第三节 物体的受力分析和受力图

3.1 受力分析和受力图

受力分析

简单地说就是分析物体的受力情况，确定物体受到哪些力，各个力的作用点在哪？作用方向是什么？是一种定型的分析。

为什么要进行受力分析

只有先定性地给出物体地受力情况，才能定量地求解各力的大小，然后才能解决其他问题。没有受力分析，求解静力学问题将会无从下手。

受力图

把物体所受到的所有力（所有的主动力和约束反力）以一种简明的图形画出来，称为画物体的受力图。

取分离体

为了把结果清晰地显示出来，把要研究的那个物体从周围的物体中分离出来，单独画它的简图，这个步骤叫做取分离体，或者叫做取研究对象，画出来的这个简图称为分离体图。

画受力图步骤

应该说画受力图没有固定的方法，但是如果遵循下面画受力图的步骤，会使画受力图变得清晰简单些：

1. 取所要研究物体为研究对象（分离体），画出其简图
2. 画出所有主动力
3. 按约束性质画出所有约束（被动）力，不要多画力，也不要少画力。

解：

1. 画出简图
   
2. 画出所有主动力
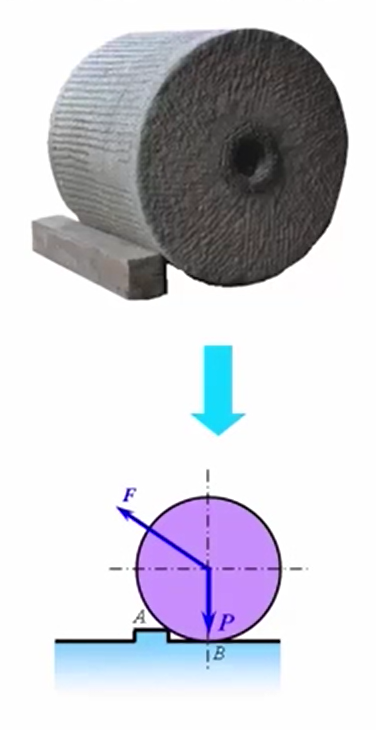
   （1）自身的重力$P$，作用点作用在碾子的中心处，方向竖直向下。
   （2）斜向上的拉力$F$，也是作用在碾子的中心处。
   
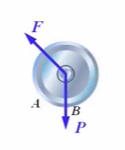
3. 依据约束的特点，画出所有约束力
   （1）B点的约束是一个光滑接触约束，它的约束力作用在接触点B，沿着公法线方向指向碾子中心。
   （2）A点的约束也是一个光滑接触约束，它的约束力作用在接触点A，沿着公法线方向指向碾子中心。
   

注意：因为A处约束是固定铰链支座与地面固定在一起，所以约束力为两个正交分力。C点是通过光滑圆柱铰链与右边连接在一起，因此也是两个正交分力。

注意：在画BC拱时，C点是带着销钉的。B处约束是固定铰链支座与地面固定在一起，所以约束力为两个正交分力。C点是受到AC拱对销钉的作用力，它与AC拱对C点的受力是一对作用力和反作用力。

注意：在以整体为研究对象时，将AC拱和BC拱所受到的力分别画出，会发现在C点处是两组相互平衡的作用和反作用力，其实C点的受力在整体的结构中它是内力，此时不画。
所研究的系统内，物体与物体未分离处相互作用的力称为内力。
内力一律不画在受力图上，绝对禁止画在受力图上。

所以整体的受力图应该这么画：

画受力图是静力学求解中非常关键的一步，如果受力图画错，后面的计算都是没有意义的，除了多加练习以外没有其他方法。

3.2 二力构件

工程中有一种很常见也很重要的构件叫做二力构件，工程中画受力图的时候要特别注意这类构件的存在。我们结合这样一个例子来说明二力构件的结构特点。

解：

1. 取CD杆为研究对象，画出简图

• 画出所有主动力
• 依据约束性质画出所有约束力
  
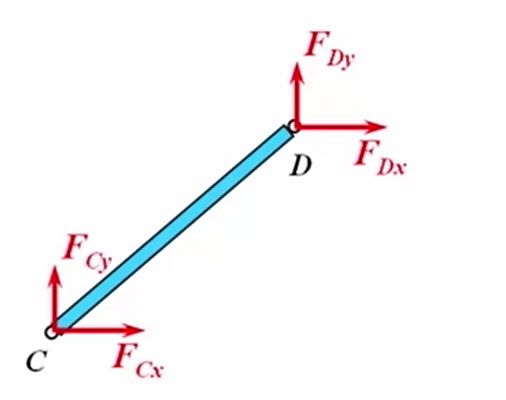
  那么这么画对不对呢？有前面关于约束的特点我们指导，D点为光滑圆柱铰链约束，本质上是光滑接触约束，本质上是一个力，C点是固定铰链约束，本质上也是一个力。因此CD杆其实处于两个力的作用下。由二力平衡公理可知，刚体上作用有两个力，使刚体保持平衡的充要条件是：这两个力大小相等，方向相反，且作用在同一直线上。因此这两个力等值、反向、共线。因此CD杆的受力是这样的，CD杆就是二力构件
  

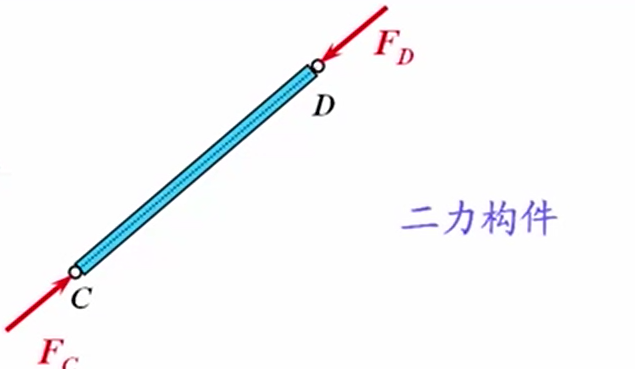
二力构件

只在两个力作用下平衡的构件，称为二力构件；若构件为直杆或弯杆，则成为二力杆。
注意：一个构件是否为二力构件仅与它的受力有关，而与它的形状无关。
二力杆（二力构件）的受力特点：两个力必定沿着两个力作用点的连线，且大小相等，方向相反。
对于直杆来说，两个力都是沿着杆的方向，大小相等方向相反，可能是压力也可能是拉力；对于弯杆来说，无论形状如何，两个力的方向必定在两个受力点之间的连线上，大小相等方向相反；对于任何形状的构件来说，只要在两个力的作用下平衡，两个力的方向都在两个受力点之间的连线上，大小相等方向相反。所以对于二力构件来说，它只有一个未知约束力，知道了一个，另一个也就知道了。

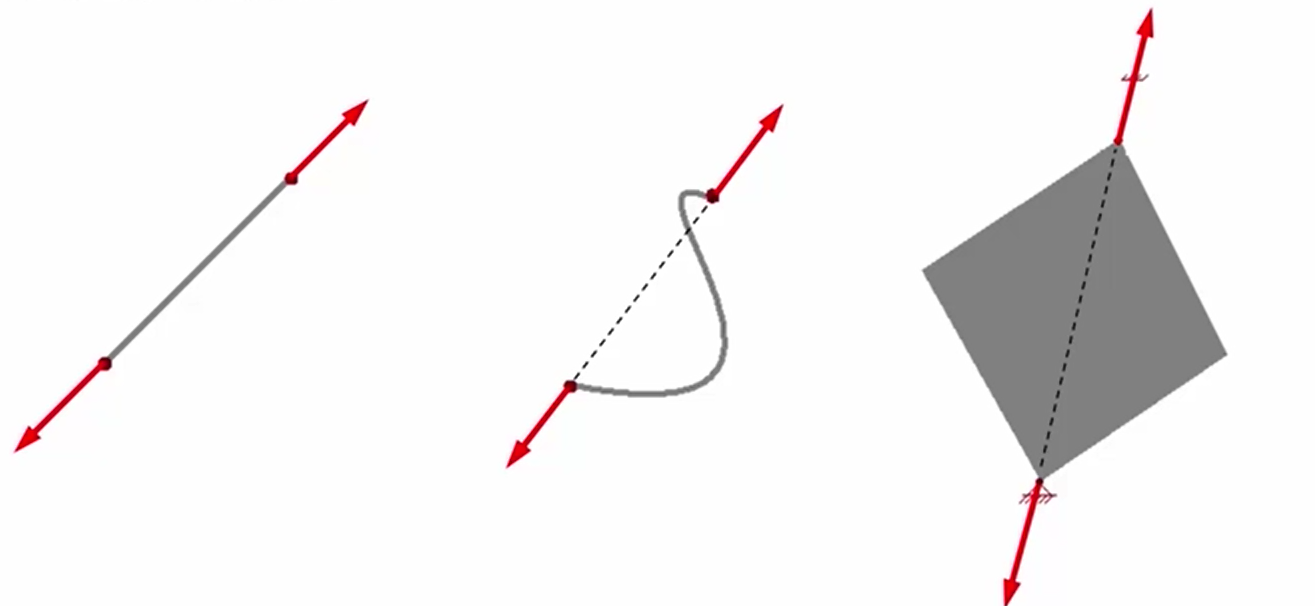
回到上述示例
2. 取AB梁为研究对象，画出简图

• 画出所有主动力
• 依据约束性质画出所有约束力
  A点受到的是固定铰链支座约束，所以它的约束力可以表示为两个正交分力
  D点处的受力其实是CD杆给D点处销钉的作用力，它和CD杆在D点处的受力是作用力与反作用力的关系。
  

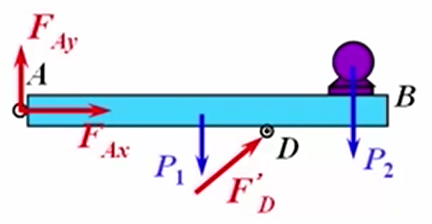
CD杆的受力图也可以画成这样，上面CD杆的受力图是受压力，现在改成了受拉力

那么此时AB梁的受力图应该这样画，D点处也是受拉力

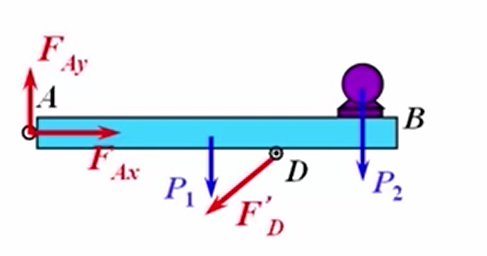
注意：通过这样一个例子我们可以看到，在画受力图的时候，不一定要给出真实的受力方向。因为在实际情况下，真实的受力方向有时很难判断，我们给出的都是假定的受力方向，真实的方向需要根据具体的计算结果来得到。

练习

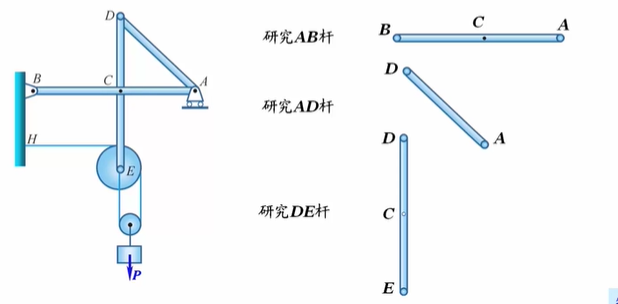
请判断下列图形中，哪些是二力构件？并画出杆上D点的受力方向

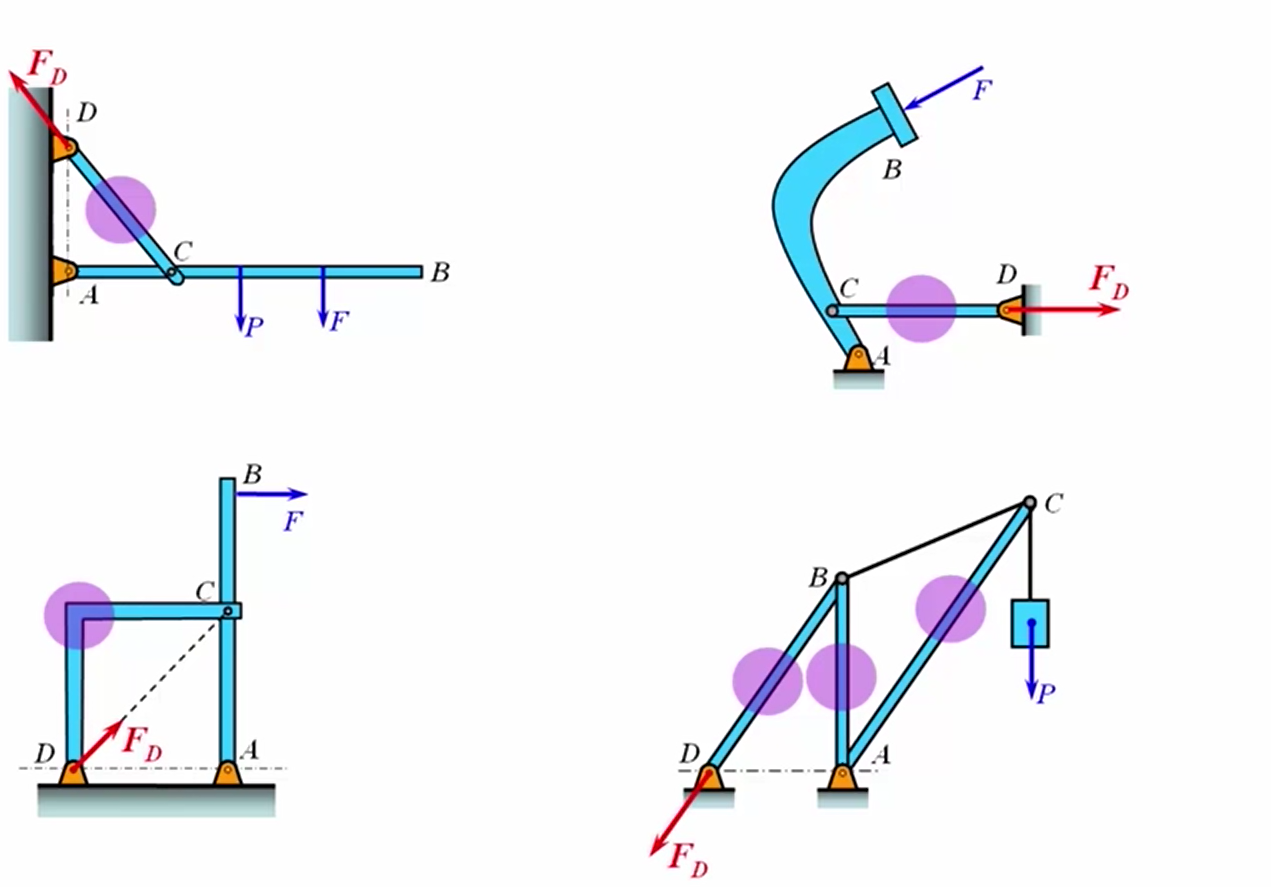
详解图4：

• 这个结构包含有三根杆，首先可以看出DB杆是一个二力杆，因为它一端通过固定铰链支座与地面连接在一起，另外一端为光滑圆柱铰链约束，这两个约束本质上都是光滑接触约束，所以DB杆是一个二力杆。
• 类似地，AB杆也是一个二力杆。
• 再来看看AC杆，在A点是固定铰链支座约束，本质上是一个光滑接触约束，是一个力，那么C点的约束可以从两个方面来考虑，一方面，如果把杆和销钉分开的话，C点其实是受到来自销钉的作用力，这是一个光滑接触约束，本质上是一个力，另外一方面，如果把销钉和杆在一起考虑的话，C点的作用力其实是作用在销钉上的两段绳子的拉力，这是两个共点力，可以合成为一个力，所以也可以看作是一个力，所以AC杆也是一个二力杆。

3.3 画受力图练习

我们通过两个例子来练习画受力图，需要着重注意画受力图的技巧以及一些注意事项

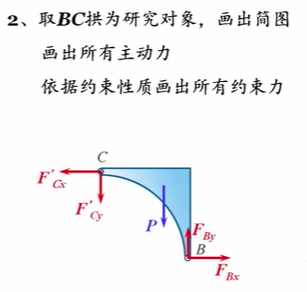
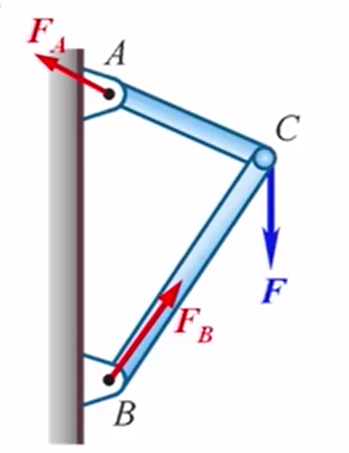
1. 首先我们来分析BC的受力，画出BC的受力图，取BC为研究对象，画出简图
2. 画出BC拱的主动力
3. 根据约束地性质画出所有约束力：B点为固定铰链支座约束，C点为光滑圆柱铰链约束，所以BC拱其实受到两个作用力，因此可以看作是一个二力构件，因此B点的约束力和C点的约束力应该是沿着两点的沿线方向，两个力大小相等方向相反。
   
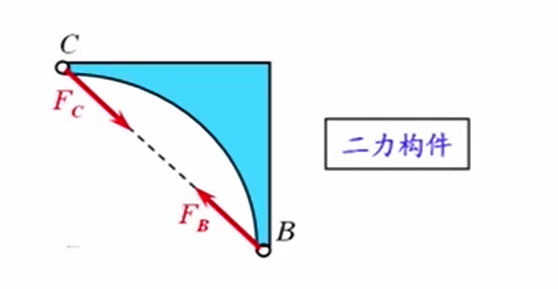
4. 我们再来看看AC拱的受力，取AC拱为研究对象，画出简图
5. 画出AC拱的主动力，主动力只有一个集中力$F$。
6. 根据约束地性质画出所有约束力：C点的约束力其实是销钉受到的来自BC拱的反作用力，它和BC拱在C点处受到的力是一对作用力和反作用力。A点的约束力按照约束的性质的话，它是一个固定铰链支座约束，应该画成两个正交的分力，但是它本质上是一个力，所以AC拱其实是受到三个力，达成平衡状态，我们根据三力平衡汇交定理知道，其中两个力$F$和$F'_C$汇交于一点，那么第三个力也汇交与这一点，并且这三个力在同一个平面上，所以A点的作用方向其实是确定的。
   
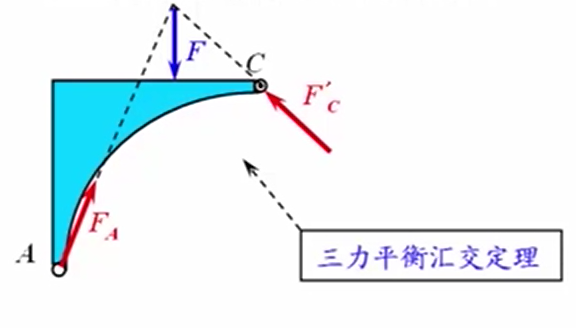
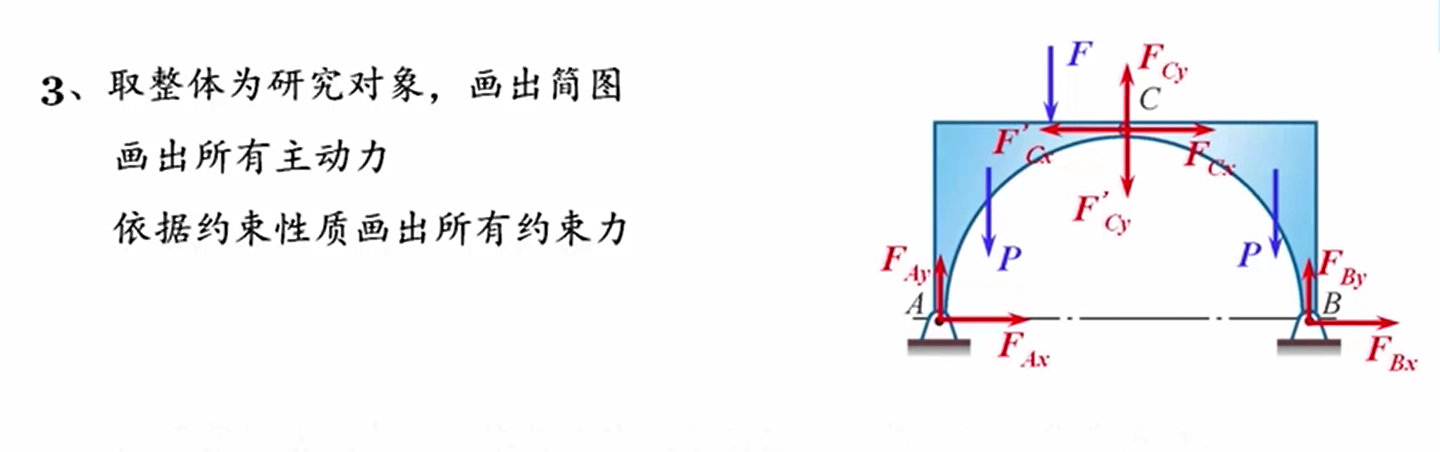
7. 取整体为研究对象，画出简图
8. 画出所有主动力，主动力只有一个集中力$F$。
9. 根据约束地性质画出所有约束力：约束力在B点的约束力方向是已知的，A点的约束力方向也是已知的，所以对整个整体的结构来说，它也是受到了三个力的作用来达到平衡，它也满足三力平衡汇交定理。
   

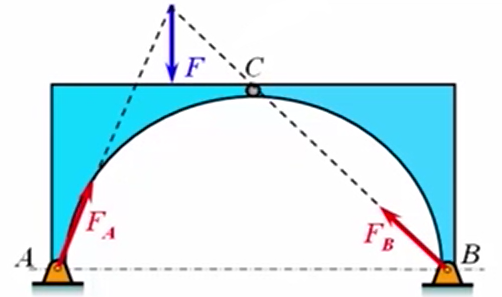
1. 取BC杆为研究对象，销钉置于AC杆上，画出简图
2. 画出所有主动力，因为不考虑杆的自重，并且销钉在AC杆上，所以没有主动力。
3. 根据约束地性质画出所有约束力：B、C点都是光滑铰链约束，所以BC杆是一个二力杆。受力图如下
   
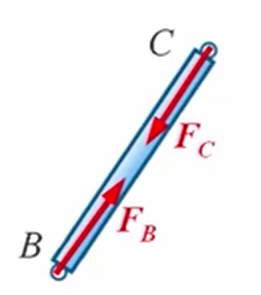
4. 取AC杆为研究对象，画出简图
5. 画出所有主动力，AC杆上有销钉，它受到主动力$F$。
6. 依据约束性质画出所有约束力：C点受到的约束力是来自BC杆的反作用力，它和BC杆在C点处受到的力是一对作用力和反作用力，是大小相等方向相反的。通过分析C点的受力我们知道，AC杆其实也是一个二力杆，它应该也是沿着杆的方向。有的同学可能有疑问：C点的受力也是沿着杆的方向吗？是的，因为C点受到的两个力的合力是沿着杆的方向的。这个合力与A点受到的力$F_A$是大小相等方向相反的，所以说AC杆仍然是二力杆。
   
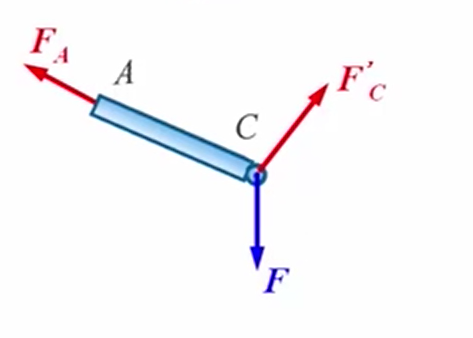
7. 取整体为研究对象，画处出简图
8. 画出所有主动力，C点处销钉受到主动力$F$。
9. 依据约束性质画出所有约束力。
   

如果取AC，BC杆为研究对象，且销钉与两杆分离的话，则：

3.4 力学模型和力学简图

理论力学所研究的问题都是从实际问题中抽象出来的模型，所面对的图形都是力学简图，如何实现从一个实际问题到力学简化模型的过程呢？涉及到力学建模，这一节介绍力学建模的过程。

力学建模

将实际问题抽象为力学模型的过程。对任何实际问题进行力学分析、计算时都要将实际问题抽象为力学模型，然后对力学模型进行分析、计算。任何力学计算实际上都是针对力学模型进行的。将实际问题转化为力学模型是进行力学计算所必须的、重要的、关键的一环，将直接影响计算过程和结果。


从这些例子可以看出，力学建模的过程也是一个简化的过程，不仅是对结构的简化，也是对载荷、约束等等多方面的简化，那么简化的原则是什么？其实这也是力学建模的原则

力学建模的原则

• 抓住关键、本质因素、忽略次要因素
• 多方面进行抽象化处理。

1. 非均匀材料假设成均匀材料，比如说碾子的材制不可能完全均匀。
2. 结构有变形但抽象成刚体，比如碾子在受力中会有变形，但是对于我们所研究的问题影响很小，我们认为它们都是刚体。
3. 三维物体有时处理成二维，比如碾子的轴向几乎不受力，因此可以不考虑轴向的尺寸，把它处理成二维的圆盘。
4. 把复杂形状简化为简单形状，比如碾子截面的形状不可能是标准的圆形，我们将它处理成光滑的圆盘，这对实际的影响不大。
5. 载荷简化成集中力或分布力，比如碾子受到的拉力作用在中心处，它的作用面是一个面，但是因为面非常小，因此简化为集中力。类似地，如果力的作用范围是作用在一个面上，或者作用在一条线上，我们可以简化为分布载荷，如果差别不大的话，我们还可以进一步简化为均布载荷。
6. 很多约束简化为理想约束，比如碾子在B点和A点都是存在摩擦力的，但是我们简化为光滑接触。
   
   通过这样的简化，一个复杂的工程实际问题就会变得相对简单。但是所产生的误差又是在可接受的范围之内，如果不进行简化，那么大部分的工程实际问题都是无法求解的，所以这样的简化、建模的过程都是非常重要的。
   这就是力学建模的概念和原则，将力学模型画出来就是力学简图。

力学简图

将力学模型用简单明了的图形来表示，这类图形称之为力学简图。
需要注意的是，很多实际结构，在简化后可能得到的是同一个力学模型，也就是说，同样一个力学简图可能对应多种实际结构。

比如这是力学结构中非常常见的一种结构叫做简支梁，梁的一端通过铰链固定在地面上，另外一端通过滚动支座可以在地面上自由地伸缩。它对应的实际结构可以是桥梁中的桥箱，也可能对应的是屋顶的一根大梁。

一个实际结构也可能简化成不同的力学模型。
一个拱桥可以简化成三铰拱桥结构，有时候简化为二铰拱桥结构。

课后习题及解析

1. 如图所示结构中，不计各杆的自重，请问AB杆的受力，画出受力分析图
   
   首先分析CD杆不带销钉，CD杆为二力杆。
   接着分析AB杆，C处带销钉，画出简图后，画出主动力$F$，由于CD为二力杆，C处受到的约束力为CD杆在C处作用力的反作用力，A处为固定支座约束，只有一个约束力，因此AB杆仅受三个力达到平衡，根据三力平衡汇交定理即可求出三个力的方向。
   

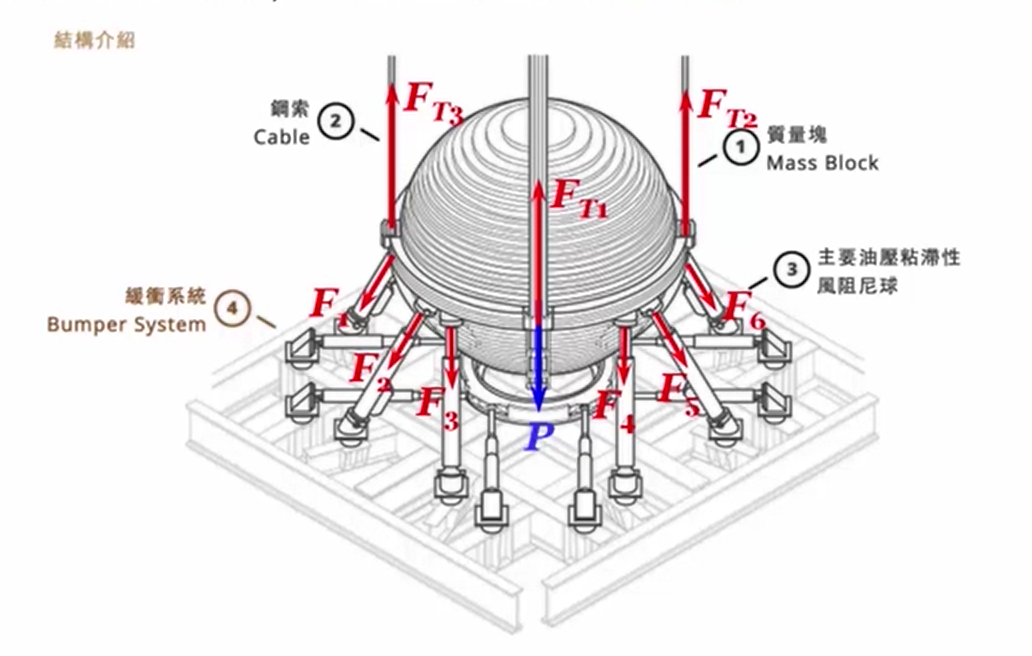
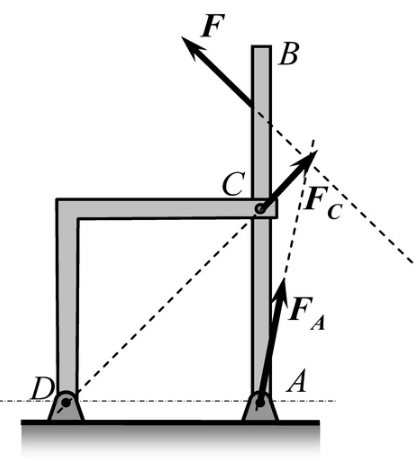
2. 如图所示结构中，不计各杆的自重，绘制整体结构的受力分析图
   
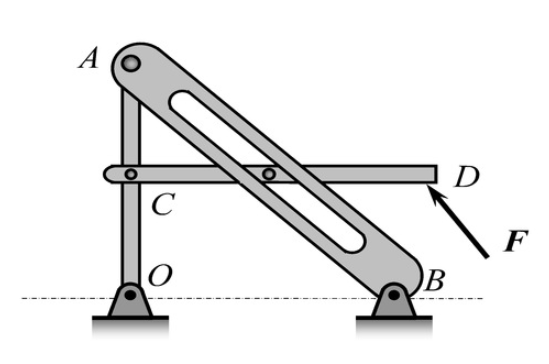
   设AB杆和CD杆中间的约束为T。首先分析CD杆，CD杆的主动力为$F$，约束T可以视作是光滑接触面约束，约束力方向垂直于AB杆指向右上方，C约束为光滑圆柱铰链约束，因此根据三力平衡汇交定理可以求出C处的约束力方向。
   接着分析AO杆，尽管C处的约束力可以求出，但是A点的受力方向无法确定，无法利用三力平衡汇交定理确定O点受力方向，因此O点处的受力需要用两个分量来表示。
   同理，对于AB杆，由于A点受力方向也无法确定，因此B点受力方向也无法确定，应用两个分量来表示。
   C、T、A处的受力均为内力，不需要绘出。
   

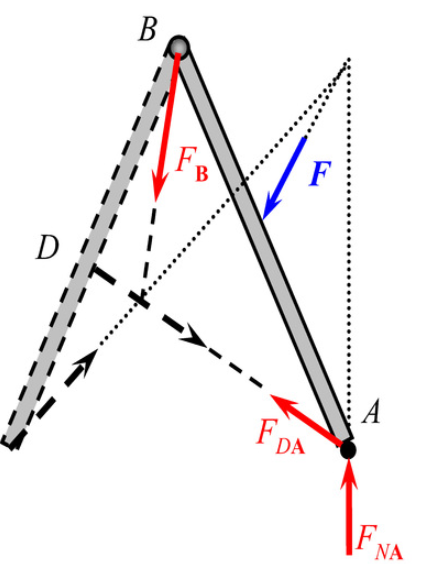
3. 图示结构中，F1作用在D点的销钉上，画出CD的受力图
   
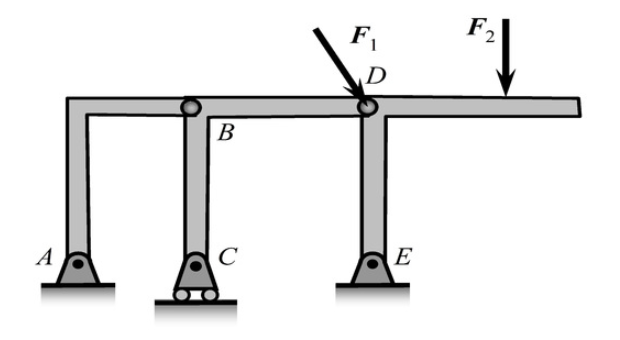
   D点连着销钉时：
   首先分析AB杆，A处为固定铰支座约束，B处为光滑圆柱铰链约束，各有一个约束力，因此AB杆为二力杆，受力方向沿着AB所在直线。
   接着分析BCD杆，首先绘出主动力$F_1$和ED杆的反作用力，因为ED杆在D点的受力方向未知，用两个正交分力表示。
   C处为滚动支座约束，构件受到垂直于光滑面的约束力$F_{NC}$，B处连接二力杆AB，因此B处受到的约束力为AB杆在B处作用力的反作用力$F_B$。D点的F1、FDx、FDy这三个力的和力与FB和FNC满足三力平衡汇交定理。
   
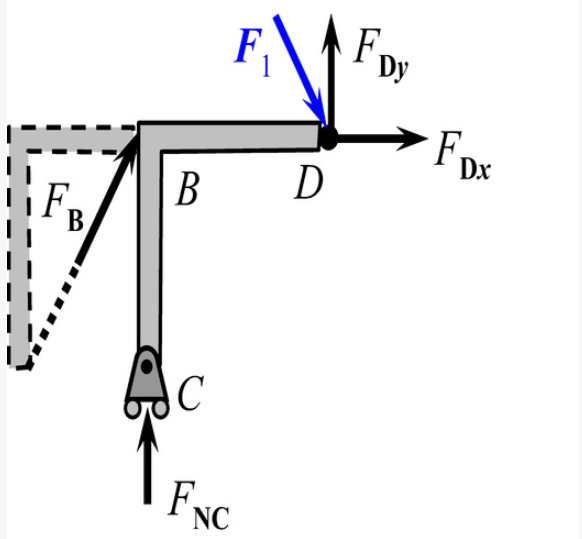
   D点不带销钉时：
   首先分析AB杆，A处为固定铰支座约束，B处为光滑圆柱铰链约束，各有一个约束力，因此AB杆为二力杆，受力方向沿着AB所在直线。
   接着分析BCD杆，D点不带销钉，因此不体现主动力$F_1$。
   C处为滚动支座约束，构件受到垂直于光滑面的约束力$F_{NC}$，B处连接二力杆AB，因此B处受到的约束力为AB杆在B处作用力的反作用力$F_B$。因此可由三力平衡汇交定理确定D处受到另一端杆件的反作用力$F_D$。
   

4. 图示结构中，绘制AB杆的受力图
   
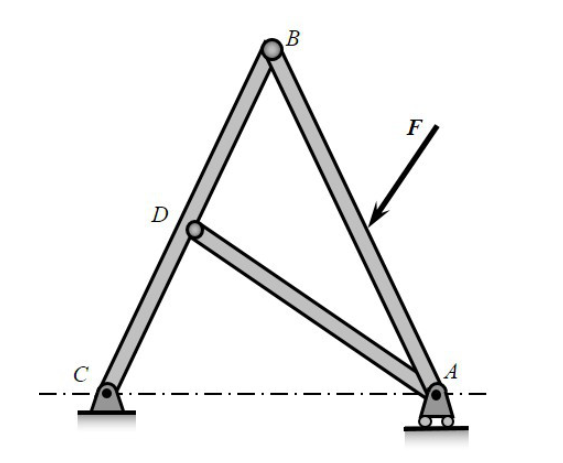
   不考虑CB杆的受力情况，单独考虑AB杆，不带销钉时，AB杆在AB两点的受力方向皆不可知，均用用两个正交分力表示。
   
   带着销钉，不考虑CB杆的受力情况，单独考虑AB杆的话，AB杆在B两点的受力方向不可知，A点为滚动支座约束，受力为销钉所受的地面支持力$F_{NA}$和二力杆AD的作用力$F_{DA}$。
   
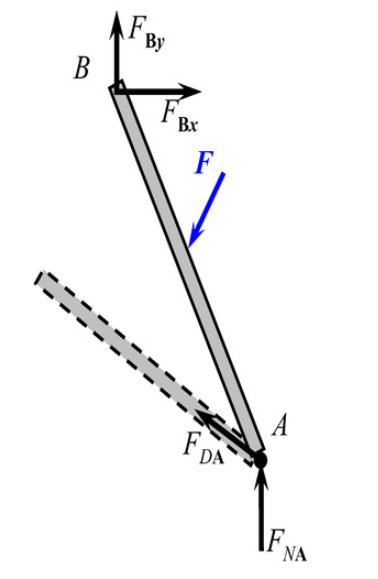
   带着销钉，考虑CB杆的受力情况的话，CB杆在C点的受力可通过整体由三力平衡汇交定理得出，由此B点的受力在CB杆上通过三力平衡汇交定理得出。故AB杆在B点的受力方向可确定。A点受力为销钉所受的地面支持力$F_{NA}$和二力杆AD的作用力$F_{DA}$。