理论力学 第四节 平面汇交力系和平面力偶系
第四节 平面汇交力系和平面力偶系
平面汇交力系合成与平衡的几何法
所谓几何法就是几何作图的方法,所以这种方法也成为图解法。在学习这个方法之前首先要了解汇交力系
汇交力系
各力的作用线都汇交于一点的力系。可分为空间汇交力系和平面汇交力系。

合力
多个力的作用线汇交于一点,如果能用一个力来等效替换,此力称为合力。简言之,如果一个力与某一个力系等效,则称此力为该力系的合力。
那么怎么来求汇交力系的合力呢?
两个共点力的合成——力三角形规则
我们知道使用力的平行四边形定则可以求出合力的大小和方向,那么如何用力三角形规则来求呢?
力是一个矢量,如果人为规定,向量的起点为力首,重点为力尾的话,那么这个线段就有了首尾之分。
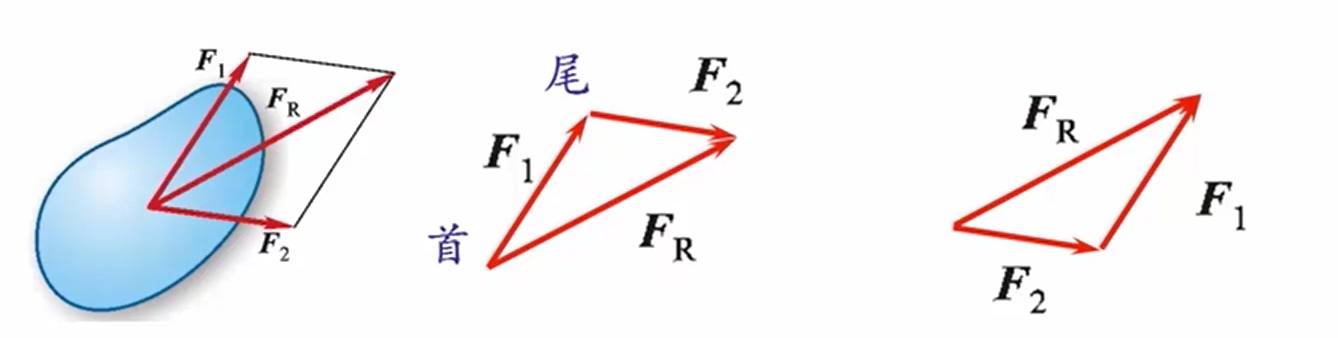
将第一个力矢量画出来以后,将第二个力矢量平移出来,将第二个力的力首与第一个力的力尾首尾相连,然后从第一个力的力首指向第二个力的力首,就是合力的矢量。规则里,第一个力和第二个力并不存在顺序问题。完全可以先画出第二个力,再画第一个力。
注意:力三角形规则求出的是合力的大小与方向,作用点仍在交汇点。
多个汇交力的合成——力多边形规则
假设在物体上有一个汇交力系,从到,它们的作用线汇交于O点,现在我们用平移定理,将所有的力都平移到O点,而不改变这个力系的作用效果。这样一来,这个汇交力系就变成了共点力系,对这个汇交力系的合成就是对共点力系的合成。
利用力的三角形规则
- 首先得到;
- 接着计算
.......
依次进行下去,就可以得到所有力的合力,把所有中间过程省略掉,就可以发现,合力的矢量其实就是从第一个力的力首指向最后一个力的力尾的连线。

这样求汇交力系的方法就被称为力多边形规则,这样一个多边形就被称为力多边形。
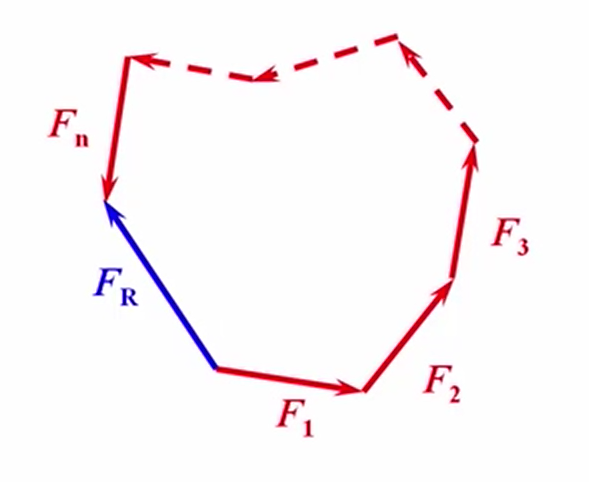
如果将这个多边形其中的任意几个力交换顺序,最后得到的合力不变。也就是说,对于一个汇交力多边形来说,它的力多边形不唯一。

注意:由力多边形规则求出的是合力的大小与方向,作用点仍在交汇点。
汇交力系平衡的几何条件
我们知道一个汇交力系可以与一个力等效,这个力就是汇交力系的合力,所以汇交力系的平衡条件就是,这个力的合力矢量为0,即。
也就是说,汇交力系平衡的充要条件是:该力系的力多边形是自行封闭的(汇交力系平衡的几何条件)。
假设力系的力多边形不自行封闭的话,那么第一个力的力首和最后一个力的力尾间是有间隙的,那么合力即为从第一个力的力首指向最后一个力的力尾,。如果没有间隙,那么合力。
注意:力多边形规则求合力和平衡的几何条件适用于任意汇交力系(平面及空间)。
求解实际问题

CD杆是一个二力杆,以AB杆为研究对象,画受力图

利用汇交力系,利用平衡的几何条件,画封闭的力三角形
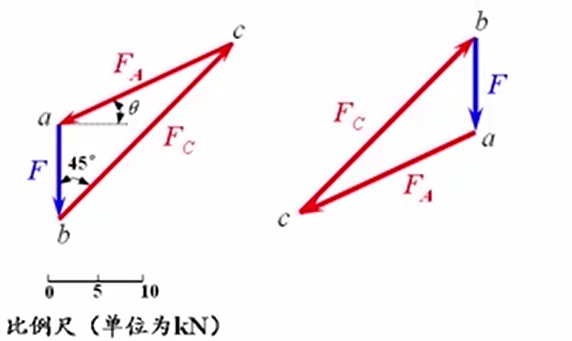
最后我们可以根据比例尺量出或根据三角函数计算出和的大小,得。
因此我们发现,利用几何法来分析起问题来,很直观也很简单,但是计算不是很方便,因此在实际问题中,这种方法应用不是很多。
平面汇交力系合成与平衡的解析法
力在直角坐标系上的投影和力沿轴的分解
假设有一个平面力,大小、方向、作用点确定,现在我们建立这样一个平面直角坐标系,与坐标轴的夹角为,将向轴做投影得到,我们知道。类似地,我们可以得到它在轴的投影,得到。这就是力矢量在直角坐标系的投影。
同时也由力的平行四边形法则,还可以将力写成两个分力的矢量和,即,这就是力沿直角坐标轴的分解。

注意:力在坐标轴上的投影一般不等于力沿着该坐标轴的分解,但是直角坐标系下二者是相等的。所以一般的静力学问题大多选择在直角坐标系下进行分析。
平面汇交力系合成的解析法
我们利用合矢量的投影定理来得到合力的投影定理。我们知道合矢量的投影定理说的是有限个矢量的和,在坐标轴上的投影等于所有矢量各自在这个轴上的投影的和。
也就是说
合力的大小为:
合力方向的余弦值分别为:
作用点为力的交汇点
平面汇交力系平衡的解析条件(平衡方程)
那么如果一个平面汇交力系平衡的话,它所满足的解析条件是什么?
我们前面学过,一个平面汇交力系平衡的几何条件是力多边形自行封闭。
我们知道平面汇交力系与它的合力是等效的,这个力系平衡的话也就意味着它们的合力为,也就是说
也就意味着这个合力在两个坐标系上的分量为,即
一个平衡力系可以列出两个独立的平衡方程,可以求解两个独立的未知量。
求解实际问题

解:
- 取研究对象。AB、BC两杆都是二力杆。通常将二力杆看成是一种约束,其受力图可以不画。假设AB杆受拉力,BC杆受压力。取滑轮B为研究对象,画受力图。
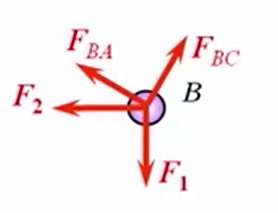
我们知道滑轮B用绳索悬吊着重物P,因此可知 - 列平衡方程求解。选取合适的坐标系如图所示,列平衡方程为:

解得
为负值,表示BA杆的受力方向与假设相反,即BA杆实际受压力;为正值,表示BC杆的受力方向与假设相同,即BC杆实际也受压力。
平面力对点的矩和平面力偶
平面力对点的矩
我们知道力可以使点发生移动,也可以使点发生转动,那么对这个转动效果的度量就是力矩。力矩不仅与力的大小有关,还与力到作用点的距离有关。
作用在平面上的一个力,如果将物体在点固定,那么力可以使物体绕点转动,这就是力对点的矩,在这里点称为矩心,而力的作用线与点所确定的平面,称为力矩的作用面,也就是说与力矢量的首尾确定的平面称为力矩作用面,而到力的作用线的垂直距离称为力臂。
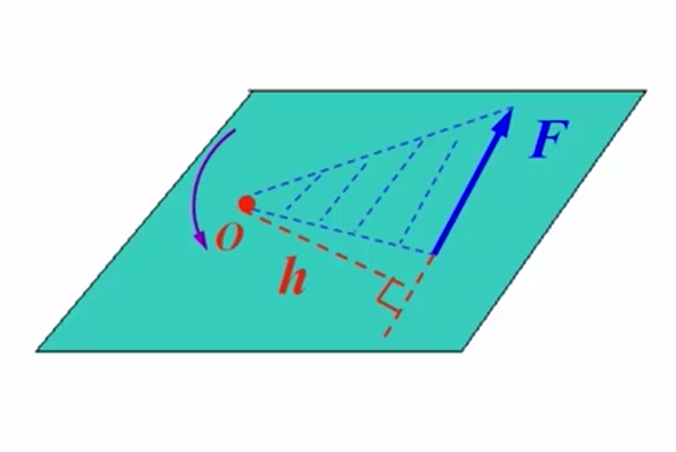
力使物体绕点的转动效果,完全由两个要素来决定:
- 大小:力与力臂的乘积
- 转向:使物体绕点转动方向
用数学公式表达:
$M_o(F) =
所以平面内力对点的矩是一个代数量,它的绝对值等于力的大小与力臂的乘积,它的正负:力使物体绕矩心逆时针转向时为正,反之为负。常用单位N.m或kN.m
合力矩定理与力矩的解析表达式
我们知道汇交力系有合力,合力矩定理就是说,这个汇交力系的合力对平面内任意一点的矩等于各个分力对这一点的矩的代数和。它提供了计算多个力对一点矩的简单方法,只需要计算它们的合力对这一点的矩就可以了,即。该结论适用于任何存在合力的力系。
假设平面内有一作用在A点的力,计算它对坐标系原点点的矩。

计算力对点的矩其实就是计算它在轴和轴的两个分量分别对点的矩。
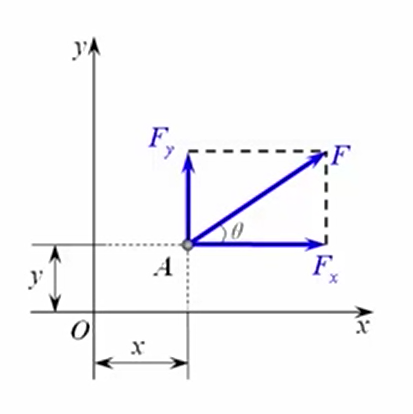
力矩的解析表达式:
= xF_y - y_F_x
如果有多个汇交力,则:
力偶
除了力矩以外,还有一类特殊的力系能够使物体产生转动效果,这就是力偶。什么是力偶呢?拧水龙头的时候,两根手指作用在开关上的力,它们是大小相等、方向相反,但是又不在同一条直线上的力。开车的时候,双手抓住方向盘,也是大小相等、方向相反,但是不在同一条直线上的两个力。

由两个大小相等(等值)、方向相反(反向)、不共线(平行)力组成的力系称为力偶,记作。力偶能对物体产生纯转动的效果。
- 两个力的两个作用线可以确定一个平面,称作力偶的作用面
- 两个力之间的距离称为力偶臂
需要注意的是
- 力偶是力系但不是平衡力系
- 力偶没有合力,不能用一个力来等效替换,也不能用一个力来平衡
- 力偶和力一样,是力学中的一个基本要素,不能再简化
力偶矩
力偶矩是对力偶使物体转动效果的度量。
平面力偶矩是一个代数量,其绝对值等于力的大小与力偶臂的乘积,正负号表示力偶的转向:一般以逆时针转向为正,顺时针转向为负。单位N·m,大小也可以用三角形(平行四边形)的面积表示。

- 大小:力与力偶臂的乘积
- 转向:作用面内的转动方向
同平面内力偶的等效定理
在同一个平面内的两个力偶,如果力偶矩相等,则两力偶彼此相等。
- 推论1 力偶可在其作用面内任意移转,而不改变它对刚体的作用。力偶对刚体的作用与力偶在其作用面内的位置无关
- 推论2 只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力的大小与力偶臂的长短,对刚体的作用效果不变。
- 力偶矩是平面力偶作用的唯一度量。也就是说,我们不关心它具体对应的力是什么样子的,而使用力偶矩的符号来表示力偶。

平面力偶系的合成和平衡条件
当有多个平面力偶,也就是说有一个平面力偶系得时候,能否像对汇交平面力系一样对平面力偶进行合成呢?如果能,结果会是什么呢?
平面力偶系得合成
已知:。
我们可以将这n个力偶矩,根据同平面内力偶的等效定理,用具有相同力偶臂长度的一系列具体的力偶来表示。
力偶臂长度d如果确定的话,则力,类似地,,。这样一来这n个力偶就变成了两个共点力系,我们可以合成为两个合力和,则有和
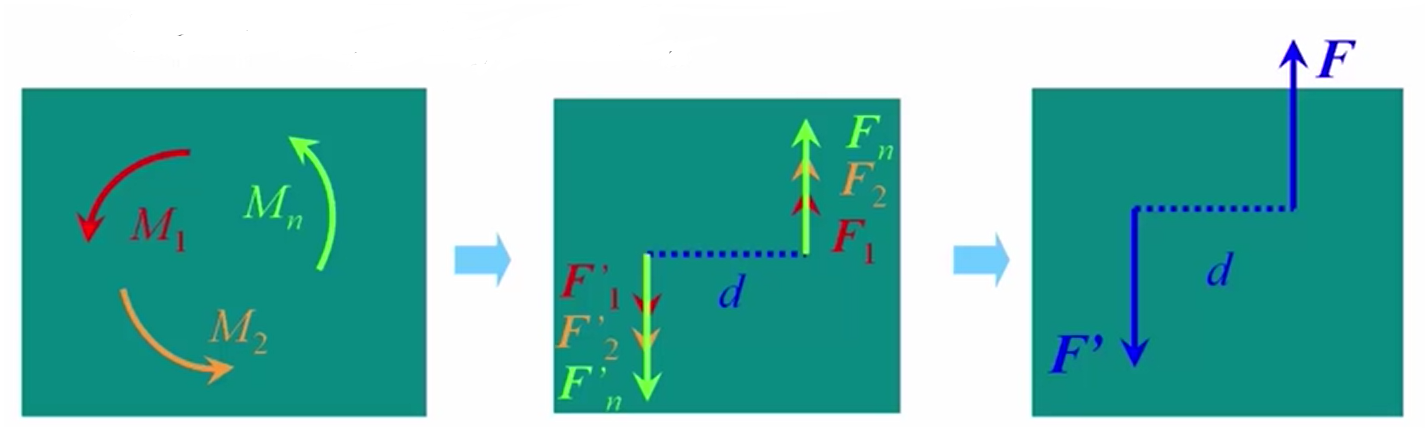
我们可以用来表示,则。
通过这样的分析过程我们可以看到,一个平面任意力偶系,可以合称为一个合力偶,合力偶的矩等于各力偶矩的代数和。
平面力偶系的平衡条件
平面力偶系平衡的充要条件:,或各力偶系的代数和等于零,。
求解实际问题

解:
- 取圆轮为研究对象,分析受力。
圆轮上作用有一个主动力,然后分析约束力,在A点受到一个遥感约束力,这是一个光滑接触约束,因此是垂直于摇杆方向的,所以说它与OA呈夹角为。O点的约束力是一个光滑铰链约束,本质上是一个约束力,那么它的方向指向哪呢?由前面我们讲到,力偶只能由力偶来平衡,因此必须与大小相等,方向相反,它们是相互平行的,构成了一组力偶,即与是平衡的。
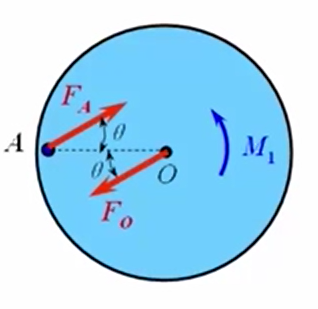
由平衡条件,得
解得
铰链在O处的约束力也就计算出来了。 - 取遥感为研究对象,分析受力。
首先遥感上有一个主动力,A点受到了销子给它的作用力,方向垂直于遥感。B点的约束力我们知道,B点为一个光滑铰链约束,所以B点是一个力,,由力偶只能由力偶来平衡我们知道,和必须构成一个力偶才能够与来平衡,所以和大小相等,方向相反。
由平衡条件,得
解得
因此,力偶只能由力偶来平衡,这是做题中隐含的已知条件。
课后习题及解析
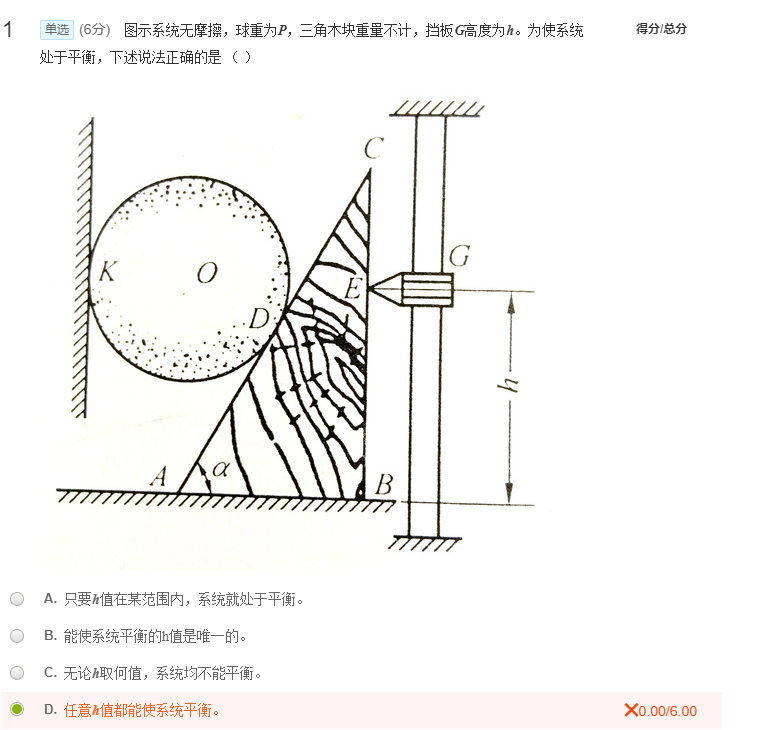
对于楔块来说,D点压力FD(垂直于斜面AC)和E点支持力FE的交点,在底面上的投影必须在底面AB上,这样地面支持力才能与这两个力满足三力平衡汇交定理。因为地面支持力,是由地面提供,必须位于地面AB上。如果超出AB,则三力无法汇交于一点,故不能达成平衡。

三个力的方向均已知,平衡的话需满足三力平衡汇交定理。
注意题目中没说不计重力要考虑重力,光滑接触面约束的约束力的方向是垂直于公切面。