理论力学 第五节 平面任意力系
平面任意力系
平面任意力系的简化
平面任意力系
力系中各力(偶)的作用线(面)处于同一平面且任意分布时,这样的力系称为平面任意力系。

武汉长江大桥,上下两个桥面的主桁架结构,它所受到的力可以近似地认为是两个平面任意力系。
哈尔滨松花江铁路桥,桥中两个主桁架所受到地内力和外力,都可以认为在这个桁架所在的平面内,构成了两个平面任意力系。

那么如何来对平面任意力系来进行简化呢?
力的平移定理
可以把作用在刚体上的点A的力平行移动到任一点B,但必须同时附加一个力偶,这个附加力偶的矩等于运来的力对新作用点B的矩。
证明:在刚体上A点作用有一个力,利用加减平衡力系原理,我们可以在B点加上一个和,它们与的大小相等,方向平行,这样就与力构成了一个力偶,利用力偶的等效定理,可以用一个力偶的符号来表示,这样就相当于,将作用在A点的力平移到了B点,并且作用效果保持不变。

- 力的平移定理提供了将力在刚体内等效移动的方法。是任意力系简化的基础,在静力学中占有重要地位。
力的平移定理的应用实例
打乒乓球时,高手容易打出弧线球,这是因为在击球过程中,拍面的法线方向与击球法向存在很大的角度,更多的是依靠拍面与球的摩擦力来使其移动,利用力的平移定理,将摩擦力平移到乒乓球的球心,为了保持力的作用效果不变,需要加上一个力偶,大小等于摩擦力对球心的矩,这样使球沿着击球方向运动,而力偶使球产生旋转。
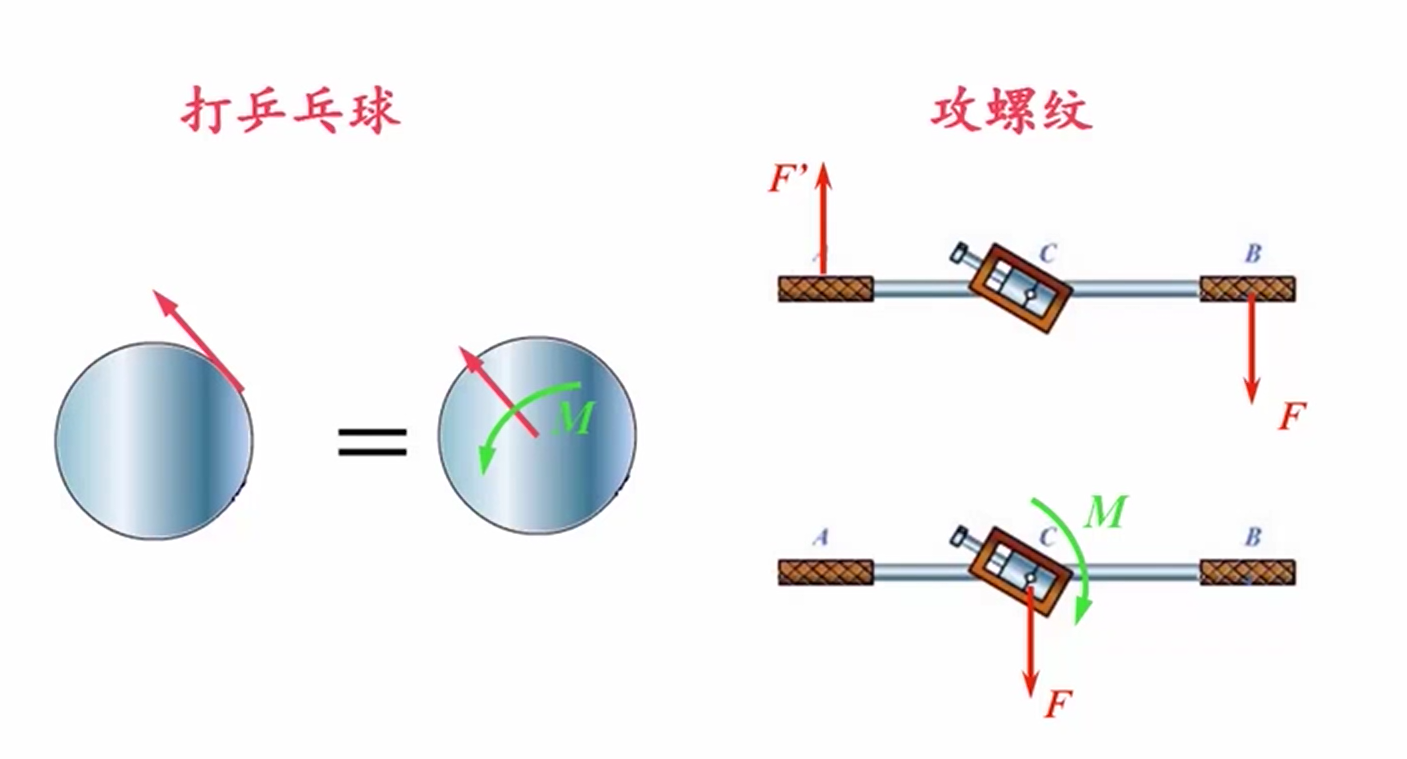
平面任意力系向作用面内一点简化 · 主矢和主矩
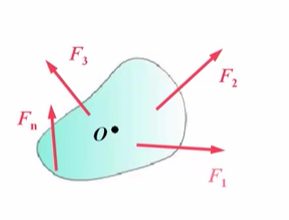
如图所示平面任意力系,将平移到O点得到,大小不变,同时需要附加一个力偶,大小等于对O点的矩。
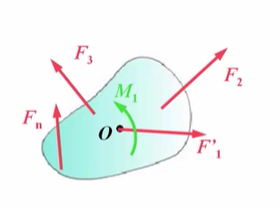
依次将所有力如此处理,得到了一个平面汇交力系,而到构成了平面力偶系。
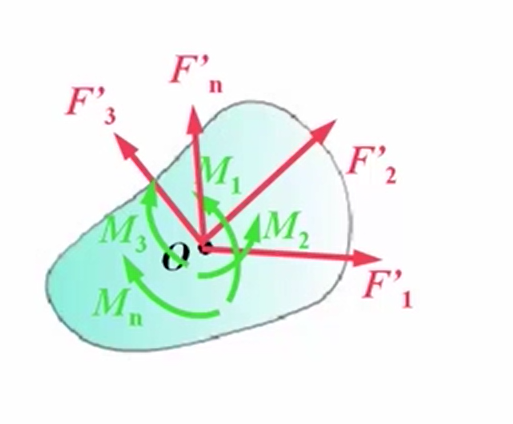
也就是说,平面汇交力系和一个平面力偶系可以等效地代替一个平面任意力系。而平面汇交力系可简化为一个合力,而平面力偶系也可以进行合成,合成为一个合力偶。即
我们不再把这个力叫做平面任意力系的合力,而是称之为平面任意力系向一点简化的主矢,即。类似地,合力偶称为平面任意力系向一点简化的主矩,即。

主矢和主矩是平面任意力系向一点简化的特征量,它们可以等效替换一个任意力系。
主矢在力系所在平面内,大小与简化中心无关。
主矩作用面也在力系所在平面内,大小一般与简化中心有关。
小结:平面任意力系向作用面内任一点O简化,可得一个力和一个力偶。力为力系的主矢,大小与简化中心无关,但作用线通过简化中心;力偶为力系对O点的主矩,作用点任意,但大小一般与简化中心有关。
主矢的计算方法一般和计算平面汇交力系的方法相同,采用解析法
主矢大小:
主矢方向:
作用点:一般令其作用于简化中心上
主矩:
平面任意力系向一点简化实例:固定端约束
埋入地下的电线杆,伸出楼面的阳台,正在车削的工件,舵机的按钮,钉在墙壁上挂东西的钉子。当他们受到来自同一个平面上的主动力时,其约束力就是一个典型的平面任意力系。这样的约束就称为平面固定端约束,它既限制了物体的移动,又限制了物体的转动。可以利用平面任意力系的简化理论,对这类约束问题进行简化求解。
为了求解这类问题,首先需要将约束端的受力进行简化,约束端的受力是个复杂并且未知的平面任意力系。不管这个力系如何复杂,我们总可以向一点,比如A点进行简化,得到一个力和一个力偶,可以用两个分量和表示,这样一来,这个复杂的任意力系可以用三个未知量来等效地替换。这样就可以很方便地求解。因此可以看来,平面固定端约束比光滑铰链约束多了一个限制的力偶。因此两个约束有本质的区别。

平面任意力系向一点简化的结果分析
第一种情况:一个平面任意力系向一点简化得到主矢和主矩,当主矢而表明简化的结果是个合力偶。如果不向O点简化,而是向平面内任意一点简化,显然主矢仍然为,因为主矢的大小与简化中心位置无关,所以向点简化,结果仍然是一个力偶,那么主矩是多少呢?因为主矢为所以平移后主矩的结果仍然是,这表明在这种情况下,该力系向任意一点简化,所得到的力系仍然是相同的力系,也就是说这其实是是一个力偶系,与简化中心位置无关。所以平面力偶系是平面任意力系的特殊情形。
前面提到过,平面任意力系向一点简化,主矢的大小和简化中心无关,而主矩的大小和简化中心有关,但是在平面力偶系的情况下,主矩大小与简化中心无关。

第二种情况:一个平面任意力系向一点简化得到主矢和主矩,当主矢而表明简化的结果是个合力,作用线过简化中心。也就是说作用在O点的力与这个力系等效,那么这个合力是否一定要作用在O点?不是的,作用在刚体上的力具有平移性,也就是可以沿着它的作用线平移,不改变作用效果,仅仅要求它的作用线通过简化中心,作用点只要存在于刚体上即可。
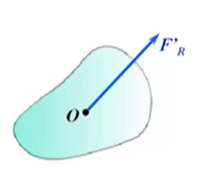
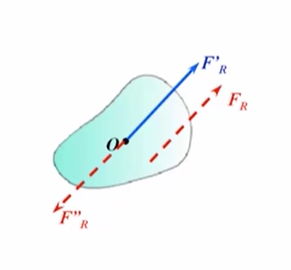
第三种情况:一个平面任意力系向一点简化得到主矢和主矩,当主矢而,利用力偶的等效定理,我们可以用和,其中和的大小与主矢相等,方向平行,力偶臂,这样就将主矢和主矩等效替换成了三个力,其中和构成了一个平衡力系,由加减平衡力系原理,因此可以将这个平衡力系拿掉,就变成了单个的力与这个力系等效,因此简化的结果仍然是一个合力,只不过作用线至简化中心有一定的距离,距离大小为。
其实主矩,,这阐述的就是合力矩定理,合力对某点的矩,等于所有分力对这一点矩的和。。
也就是说该情况简化为了作用线不过简化中心的合力。
第四种情况:一个平面任意力系向一点简化得到主矢和主矩,当主矢而,这表明了不需要任何力或者是力偶来与这个力系等效,表明这个力系自身就是平衡的,既然平衡的话,与简化中心的位置无关。
因此,平面任意力系简化的最后结果只能是合力、合力偶、平衡三种情况。
| 总结 | ||||
|---|---|---|---|---|
| 结果 | 合力偶 | 合力 | 合力 | 平衡 |
| 特点 | 该力系向任意一点简化,所得到的力系仍然是相同的力系(力偶系) | 作用线过简化中心,也就是可以沿着它的作用线平移,不改变作用效果 | 作用线不过简化中心的合力,作用线至简化中心有一定的距离,距离大小为 | 表明了不需要任何力或者是力偶来与这个力系等效,这个力系自身就是平衡的 |
| 简化中心 | 与简化中心无关 | 作用线过简化中心 | 作用线距简化中心有一定距离 | 与简化中心无关 |
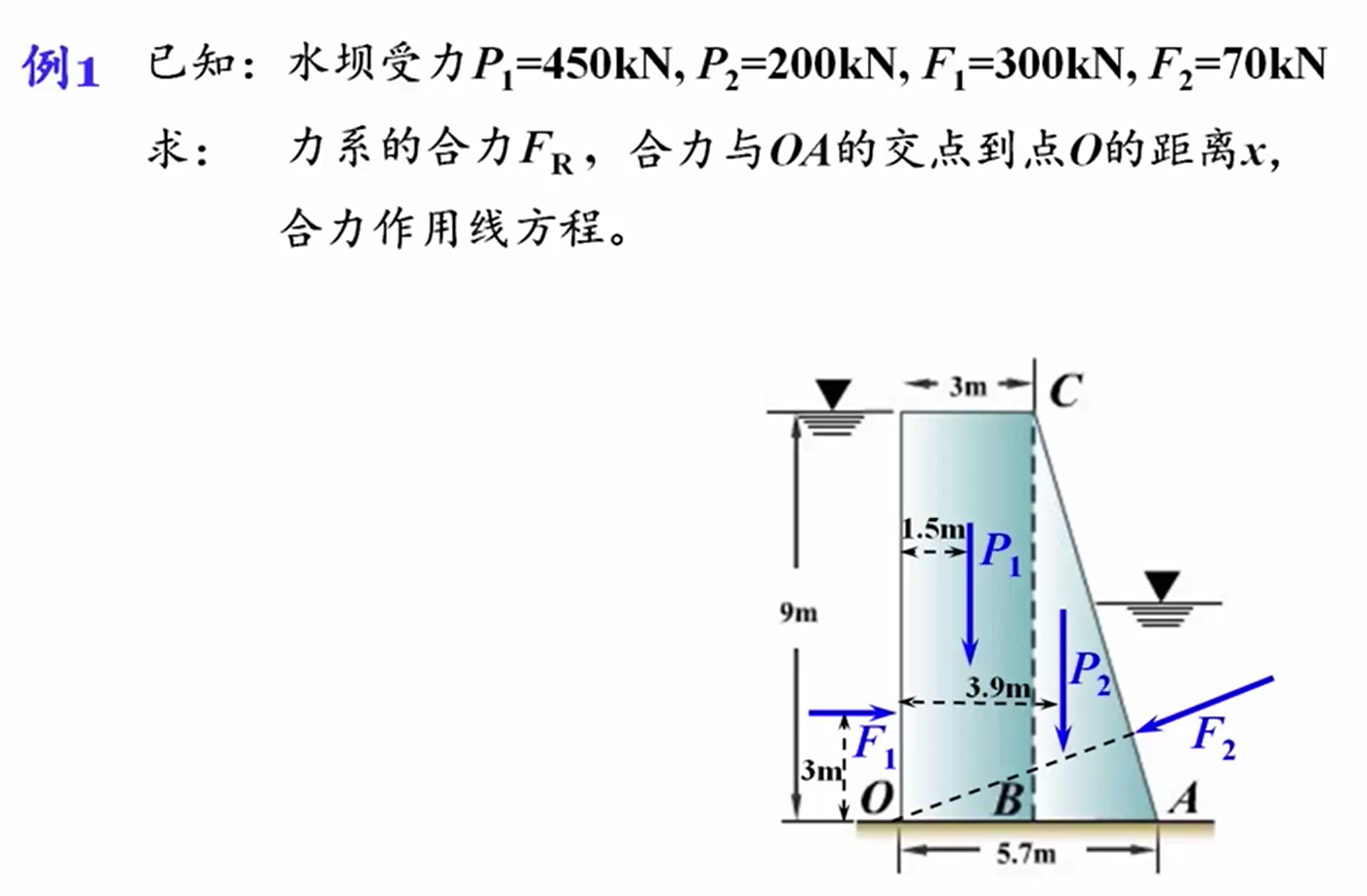
解:
- 建如图所示坐标系,向O点简化。
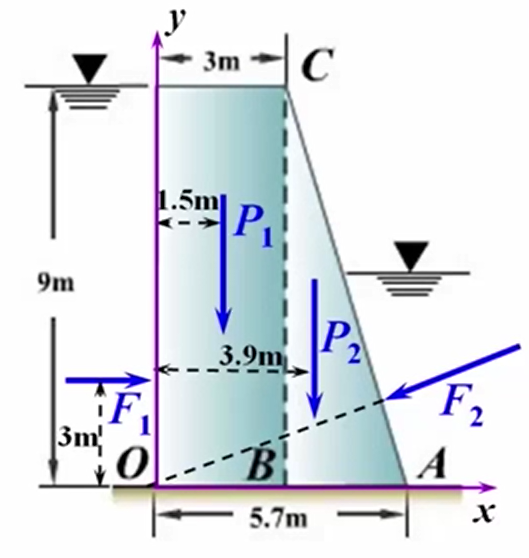
通过前面的分析我们知道,并不是一个任意力系向任意一点简化都能得到一个合力,只是在某些特殊的位置,结果才可能是一个合力。目前我们还不知道具体是哪一点,但是为了简单,我们可以首先将这个力系向O点简化,得到向这一点转化的主矢和主矩。
力系中比较特殊,首先我们确定与轴的夹角,由几何关系可知
主矢的计算方法,先分别计算主矢在轴和轴上的投影
主矢的大小为:
主矢的方向余弦分别算得:
得到主矢与轴正向夹角为,主矢与y轴负向的夹角为

注意:在求力矩的时候,就要先看一个力绕作用点是顺时针还是逆时针,顺时针就是负的,逆时针就是正的。
主矩的大小
主矩为负值,表明主矩是顺时针的,这样力系向O点简化的主矢和主矩都求出来了。
2. 求合力及作用线位置
向O点简化得到的主矢和主矩可以进一步简化得到一个合力。这个合力的大小、方向与主矢是相同的,合力的作用线到O点的距离为
那么合力的作用线到O点的距离由几何关系很容易得到
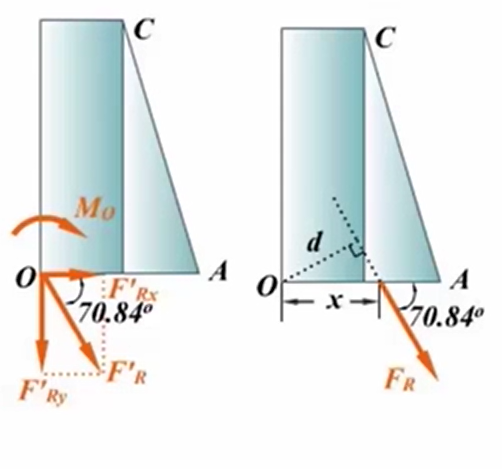
3. 求合力作用线方程
合力显然可以沿着它的作用线上下移动,不管作用在哪个点,它的效果是一样的,它的力到O点的矩总是保持不变的,等于力系向O点简化的主矩,因此可由这个关系列出合力作用线方程
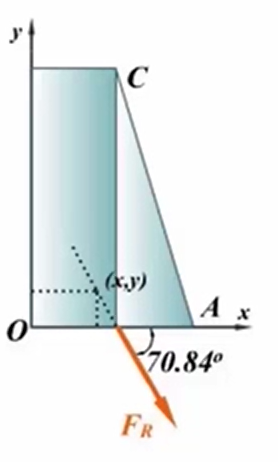
即
有
平面任意力系的平衡条件和平衡方程
如果刚体在一个平面任意力系的作用下平衡的话,平衡的条件是什么呢?
平面任意力系的平衡方程
由上一节平面任意力系的简化结果我们知道,平面任意力系的简化结果是一个主矢和一个主矩,但主矢和主矩同时为0时,这个力系平衡,并且与简化中心无关。也就是说力系平衡的话,向任意一点简化,都是相同的结果。
因此平面任意力系平衡的充要条件:力系的主矢和对任意点的主矩都等于零。