ALG_Metaballs

Introduction

ALG_Metaballs is an plug-in to generate 3d metaballs for Grasshopper using Marching Cubes algorithm on GPU. The development of this project is an important learning experience for me. I hope it can be a parallel programming reference case which can help GPU programming beginners and Grasshopper developers.

At present, its computational performance can still be optimized. I will continue to improve it in my future work.

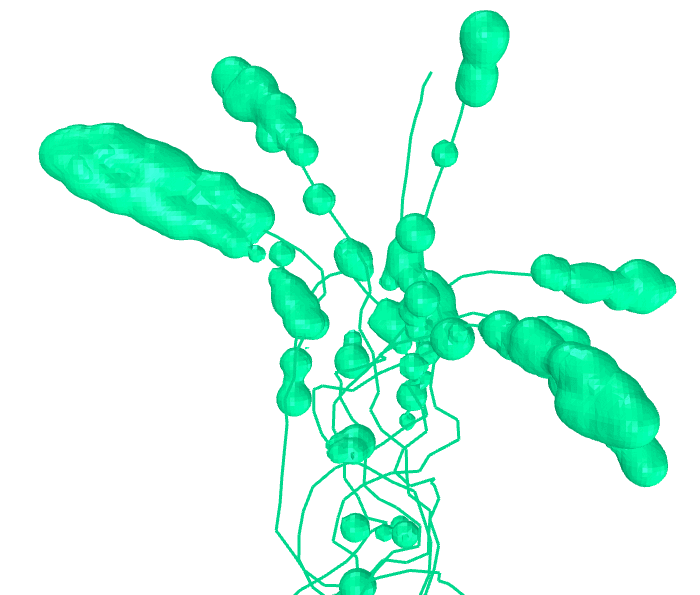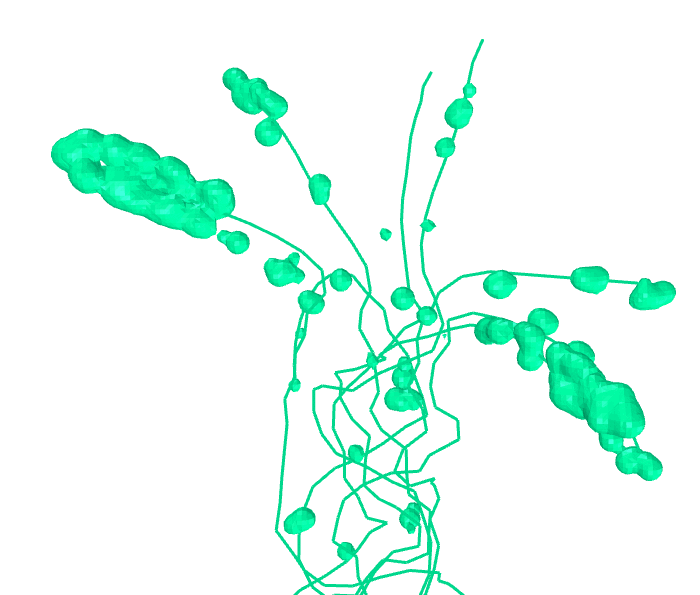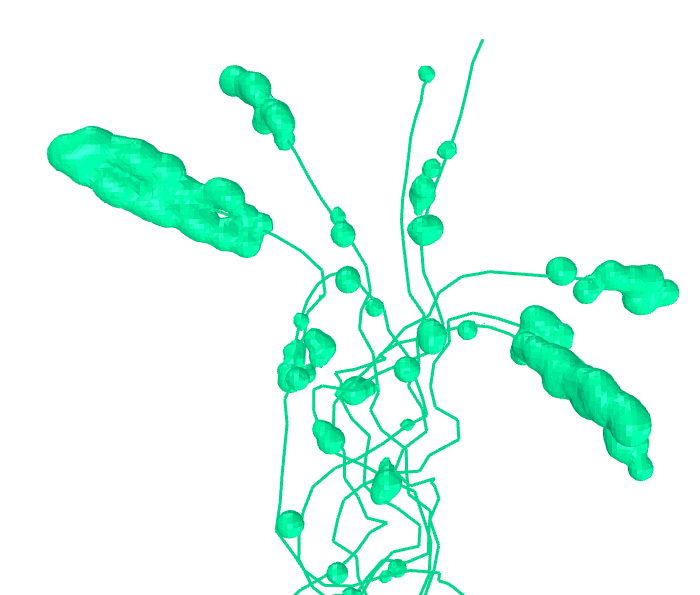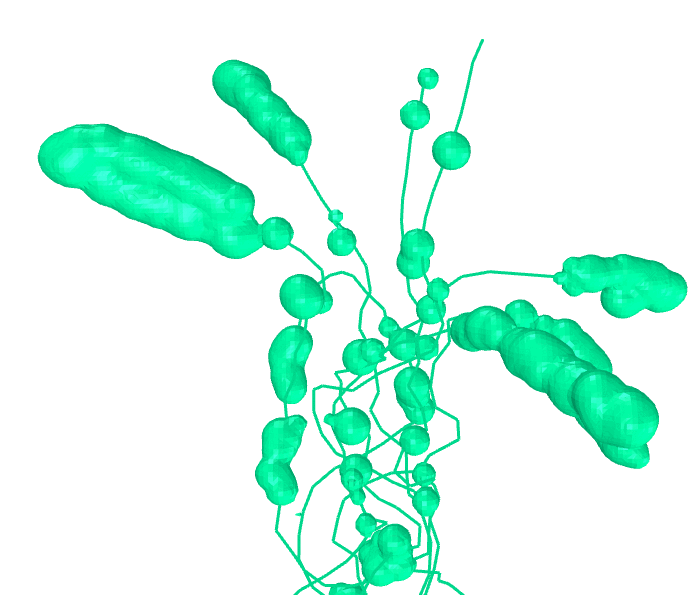
Algorithm

1. Compute bounding box from input points.

2. Generation of a voxel-based grid inside the box.

3. Classify voxels: Mark all the active voxels to get an active voxels array and calculate the number of vertices in each voxel by looking up vertices table. It is executed using one thread per voxel.

4. Exclusive sum scan: Get the total number of active voxels and the total number of resulting vertices using exclusive scan algorithm. They are obtained by the sum of the last value of the exclusive scan and the last value of input array.

5. Compact voxels: This compacts the active voxels array to get rid of empty voxels. This allows us to execute Isosurface Extraction on only the active voxels.

6. Isosurface extraction: Calculate the position of the points in the active voxel and obtain all the result points by looking up triangle table.

7. Generate a mesh model from result points.

How metaballs work [10]

Each metaball has a "sphere of influence". When you merge two metaballs and they extend into each other’s sphere of influence, they react in a way similar to drops of water: the surface tension works to form a smooth bridge between them. This is useful for making organic "blobby" shapes which meld into each other.

Metaballs can be thought of as spherical force fields whose surface is an implicit function defined at any point where the density of the force field equals a certain threshold. Because the density of the force field can be increased by the proximity of other metaball force fields, metaballs have the unique property that they change their shape to adapt and fuse with surrounding metaballs. This makes them very effective for modeling organic surfaces. For example, below we have a metaball. The surface of the metaball exists whenever the density of the metaball’s field reaches a certain threshold:

When two or more metaball force fields are combined, as in the illustration below, the resulting density of the force fields is added, and the surface extends to include that area where the force fields intersect and create density values with a value of one.

Reference

[1] Lorensen W E, Cline H E. Marching cubes: A high resolution 3D surface construction algorithm. ACM SIGGRAPH Computer Graphics. 1987;21(4)

[2] The algorithm and lookup tables by Paul Bourke httppaulbourke.netgeometrypolygonise：http://paulbourke.net/geometry/polygonise/

[3] Triquet, F., Meseure, P., & Chaillou, C. (2001). Fast polygonization of implicit surfaces.

[4] McPheeters, G. W. C., & Wyvill, B. (1986). Data structure for soft objects. The Visual Computer, 2(4), 227-234.

[5] https://www.sidefx.com/docs/houdini/nodes/sop/metaball.html